浅析莫队算法的时间复杂度

这篇文章来记录一下莫队算法时间复杂度的简单(不严谨)计算

首先分析一下莫队算法的时间复杂度有哪些方面构成

1. 对询问Query数组的排序
2. 区间左指针的移动
3. 区间右指针的移动

时间复杂度

每个add/del操作的复杂度为$O(1)$

1. 排序使用sort可以在$O(n\log n)$内完成

2. 由于左指针在排序中被分块,所以又分为块内移动和块间移动

   • 块内: 设每块中含左端点$x_i$个,由于每块大小为$\sqrt{n}$,所以在块内移动的最坏复杂度为$O(x_i\sqrt{n})$。
     因此对于所有块,将复杂度求和,即为$O(\displaystyle\sum_ix_i\sqrt{n})=O(n\sqrt{n})$
   • 块间: 左指针在每个块内移动之后,需要移动到下一个块内的左端点处,块间跳转最坏跨两个整块需要$O(2\sqrt{n})$。
     总共需要跨$\sqrt{n}-1$个块,所以复杂度为$O((\sqrt{n}-1)\times 2\sqrt{n})\sim O(n)$

综上,左指针移动的复杂度为$O(n\sqrt{n})$
3. 当左指针在同一个块内时,右指针是有序的,因此当左指针在同一个块内时,右指针移动的最坏复杂度为$O(n)$即全部移动一遍。而每个块长度为$\sqrt{n}$,总长为$n$,所以一共$\sqrt{n}$个块,所以最坏复杂度为$O(n\sqrt{n})$

综上,普通莫队算法的时间复杂度为
$$
O(n\log n)+O(n\sqrt{n})+O(n\sqrt{n})\ \sim\ O(n\sqrt{n})
$$

玄学的奇偶排序优化

见图: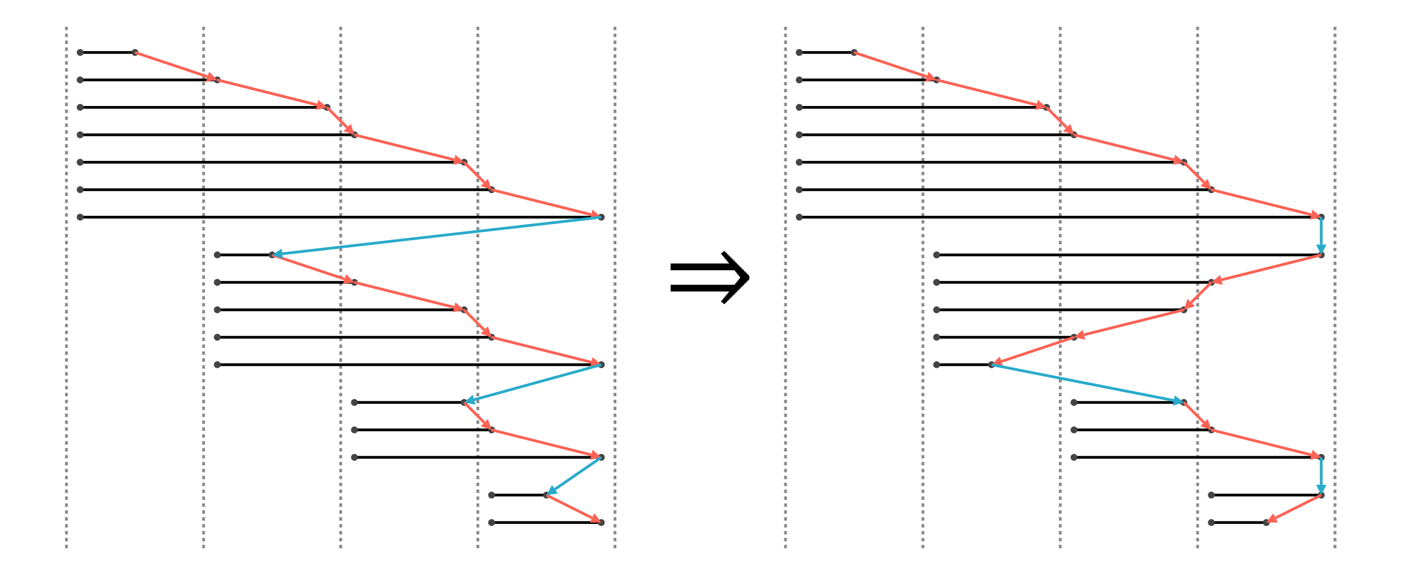

分块大小不为$\sqrt{n}$

还是和前面一样推复杂度,设块大小为$a>1$

1. 排序: 需要$O(n\log n)$
2. 左指针移动:
   • 块内: $O(\displaystyle\sum_ix_ia)=O(na)$
   • 块间: $O((\dfrac{n}{a}-1)\times 2a)=O(n)$
3. 右指针移动: $O(n\times \dfrac{n}{a})=O(\dfrac{n^2}{a})$

综上,总的复杂度为$O(n\log n)+O(na)+O(n)+O(\dfrac{n^2}{a})=O(na+\dfrac{n^2}{a})$
根据均值不等式,若让上式复杂度最小,则需要$na=\dfrac{n^2}{a}$,即$a=\sqrt{n}$
所以当含有左右两个指针时,分块大小为$\sqrt{n}$时总复杂度最小,为$O(n\sqrt{n})$

带修莫队(三指针)

还是设分块的大小为$a>1$,注意带修莫队排序优先级:先左端点所在块,再右端点所在块,后时间戳大小

1. 排序: $O(n\log n)$
2. 左指针移动: 同上推导,复杂度为$O(na)$
3. 右指针移动: 相同右端点的块的复杂度同上$O(na)$,还有换左端点决定的块时的复杂度约为$O(\dfrac{n^2}{a})$
4. 时间戳移动: 由排序优先级可见,只有当右端点所在块相同时才会移动时间戳,而每次移动最坏需要移动$\sum t \sim n$
   对于每个左端点相同的块,右端点块数为$\dfrac{n}{a}$,左端点有$\dfrac{n}{a}$个,所以一共需要$O(\dfrac{n}{a}\times\dfrac{n}{a}\times n)=O(\dfrac{n^3}{a^2})$

综上,总的复杂度为$O(n\log n)+O(na)+O(na)+O(\dfrac{n^2}{a})+O(\dfrac{n^3}{a^2})\ \sim\ O(na+\dfrac{n^2}{a}+\dfrac{n^3}{a^2})$

由于$1<a<n$,所以$\dfrac{\dfrac{n^2}{a}}{\dfrac{n^3}{a^2}}=\dfrac{a}{n}<1 \Rightarrow \dfrac{n^2}{a}<\dfrac{n^3}{a^2}$,所以原式可化为$O(na+\dfrac{n^3}{a^2})$

根据均值不等式,当$na=\dfrac{n^3}{a^2}$时上式最小,即$a=\sqrt[3]{n^2}=n^{\frac{2}{3}}$
所以含有三个指针时,分块大小为$n^{\frac{2}{3}}$时总复杂度最小,为$O(n^{\frac{5}{3}})=O(n\sqrt[3]{n^2})$